Il titolo è una chiara citazione di quei famosi manuali dove viene spiegato un argomento, magari complesso, con parole semplici, affinché risulti comprensibile anche dai principianti. Oggi cercherò di ottenere un risultato analogo parlando di f/stop (o misura dell’apertura del diaframma) e della differenza tra questo ed il più “reale” t/stop. L’argomento risulta solitamente un po’ ostico per i neo-fotografi perché utilizza una scala particolare e per spiegarlo sarà necessaria qualche breve incursione nel campo matematico.
Una prima particolarità della scala dei diaframmi è che più il numero è basso più l’apertura del diaframma sarà “grande”. Qui rappresentata vediamo una sequenza di diaframmi ad intervalli “pieni” (o meglio unitari):
1 / 1,4 / 2,0 / 2,8 / 4 / 5,6 / 8 / 11 / 16 / 22
Per quanto sopra detto, passando da f/4 ad f/5.6 non si incrementa l’apertura, ma si diminuisce. Anzi, più precisamente, si dimezza. Al decrescere del numero su quella scala si raddoppia invece la quantità di luce che arriva sul sensore nello stesso arco di tempo. Ciascun numero di questa sequenza rappresenta uno stop ed il passaggio dall’uno all’altro porta per definizione al dimezzamento/raddoppio della luce, in modo inversamente proporzionale alla grandezza del numero.
Il significato di questo bizzarro comportamento risiede nel rapporto tra il diametro dell’apertura dell’obiettivo e la sua lunghezza focale. Proprio questo rapporto è chiamato f/stop, ma andiamo a vedere perché a numeri più piccoli corrisponde quantità di luce maggiore.

Un obiettivo 50mm impostato su f/2 avrà un diametro dell’apertura di 50mm / 2 = 25mm. Le lamelle del diaframma (generalmente vanno da 6 a 14) formano un’area circolare la cui superficie possiamo calcolare con la semplice formula:
![]()
Ipotizzando di impostare il suddetto 50mm su f/2 e poi su f/2.8, possiamo verificare concretamente la maggiore “grandezza” dell’apertura f/2, ricordandosi che nella formula va inserito il raggio e non il diametro, per cui si dovrà dividere per due il valore precedentemente calcolato. Per 50mm a f/2.8 il diametro sarà di 50 / 2.8 = 17,86mm ed il raggio 17,86 / 2 = 8,9332 mm. Calcoliamo le rispettive aree;
50mm f/2.8
![]()
50mm f/2
![]()
Risulta così evidente che ad un f/stop più basso corrisponde un’area maggiore e di conseguenza un’apertura più grande dove la luce può passare, attraverso l’obiettivo, e raggiungere la pellicola (o sensore digitale).
Ma come mai si usano numeri così “strani” come 1.4 / 2 / 2.8 / ecc..? La motivazione risiede in una formula matematica non troppo complicata: i valori sono ottenuti dalla radice quadrata di 2 elevata ad un numero incrementale (ovvero un semplice progressivo 0, 1, 2, ecc..).
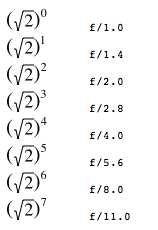
Esistono però anche valori di f/stop non “interi”, anch’essi ottenibili con la medesima formula:

Come avrete capito l’f/stop è una misura prettamente geometrica e non ci dice esattamente la quantità di luce che arriva sul sensore. Gli obiettivi sono composti da molti gruppi di lenti che pur essendo “trasparenti” assorbono comunque una minima quantità di luce, impattando negativamente sul rendimento reale. Più affidabile è concreta è la scala t/stop che misura precisamente la quantità di luce che passa attraverso le lenti con le differenti aperture. Nella fotografia questa differenza è importante, ma lo è molto di più nel campo video dove gli obiettivi (come quelli Zeiss per il videomaking) presentano questa scala in sostituzione della più classica f/stop.

In sostanza gli obiettivi trasmettono solo una porzione della luce calcolata tramite l’area geometrica dell’apertura (f/stop), quindi il t/stop sarà leggermente differente. Supponendo di avere un 50mm f/1.2 che riesce a trasmettere il 70% della luce che passa attraverso le lenti, il suo t/stop sarà di 1.8.
La riduzione di luminosità dettata dal passaggio della luce attraverso diversi “mezzi” all’interno dell’obiettivo (vetro, aria, vetro, ecc..) non va ad influenzare ulteriormente il rendimento. Ad esempio la DoF (o PdC = “Profondità di campo” in italiano) rimane comunque quella di un f/1.2 anche se catturerà la quantità di luce equivalente ad f/1.8. Volendo utilizzare un esempio reale, possiamo confrontare due lenti fisse (24mm f/1.4) top di gamma di Nikon e Canon in un grafico di DxOMark:
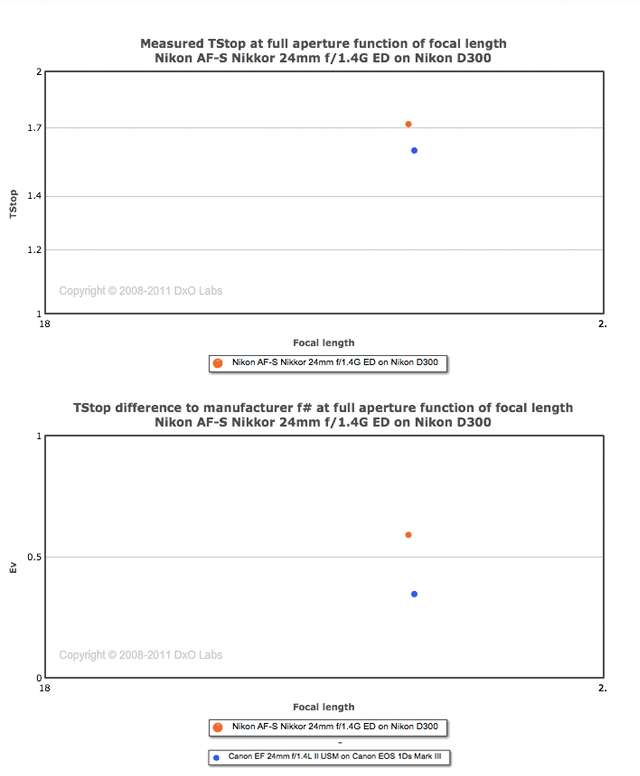
L’obiettivo Nikon ha un t/stop leggermente peggiore, anche se entrambe le lenti vengono vendute come f/1.4. Ciò non vuol dire che l’ottica Canon sia migliore o che quella Nikon sia da buttare, tuttavia hanno un rendimento leggermente diverso. In verità le differenze nella scala f/stop – t/stop sono genericamente piuttosto marginali, al punto che quasi mai vengono considerate come un parametro primario. Tuttavia la conoscenza di questa caratteristica può essere utile a valutare l’effettivo rendimento di un obiettivo.
Per utilizzare in modo corretto l’apertura non è ovviamente necessario fare calcoli “sul campo” ed anche se la scala può sembrare ostica vi garantisco che dopo pochissimo tempo di pratica risulta di immediata comprensione. Ma perché variare l’apertura del diaframma? La considerazione più immediata è relativa alla quantità di luce ottenibile e quindi alla conseguente esposizione della foto (più luce = chiara / meno luce = scura). Ma non si tratta solo di questo, perché vi è una diretta correlazione anche tra gli altri parametri di scatto (tempo e sensibilità), nonché la variazione di uno dei principali aspetti caratteristici di una fotografia, ovvero la profondità di campo di cui parleremo in un prossimo articolo.
 Oltre a richiedere rispetto ed educazione, vi ricordiamo che tutti i commenti con un link entrano in coda di moderazione e possono passare diverse ore prima che un admin li attivi. Anche i punti senza uno spazio dopo possono essere considerati link causando lo stesso problema.
Oltre a richiedere rispetto ed educazione, vi ricordiamo che tutti i commenti con un link entrano in coda di moderazione e possono passare diverse ore prima che un admin li attivi. Anche i punti senza uno spazio dopo possono essere considerati link causando lo stesso problema.